育てたい資質や能力
1 物体に働く力がつり合っていると速も向きも変わらないという見方や考え方を育てる。
2 物体に働く力がつり合っていないと速さや運動の向きが変わるという見方や考え方を育てる。
学習のポイントと配慮事項
バスがカーブを曲がったり,ボールを投げたりするときの運動は,日常生活と関連の深い分野にもかかわらず間違った概念をもっていることが多い。整理して理解させる必要がある。
理論的な背景・注意事項
1 速度と加速度
(1) 速度とはベクトルで,大きさ(速さ)と向きをもつ。
(2) 加速度は単位時間(1秒間)の速度の変化と定義される。速度はベクトルであるから図で表すと次のようになる。
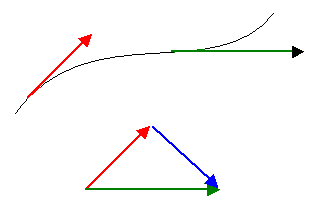
ある時刻に赤で示した速度であった物体がt(s)後に緑で示した速度になったとすれば,その間の速度の変化は青のベクトルとなり,これがこの間の加速度の向きとなる。
加速度の大きさは青の長さをtで割ったものとなる。
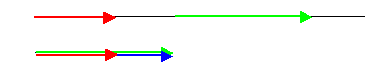
一直線上の場合はベクトルの成分で簡単に計算できる。たとえば始め10m/sで2秒後に20m/sになったとすれば加速度は5m/s2である。
物体に働く力の「合力F」と物体の質量m,物体に生じる加速度αの間には
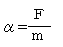
の関係がある。αとFの向きは同じ向きである。これはニュートンの運動の第二法則(運動方程式)である。
αとFはベクトルであるから,速度の向きと加速度の向きは等しい。
ここで,F=0ならばα=0すなわち等速度運動を表す。これは運動の第一法則(慣性の法則)を表している。
円運動の加速度は詳しい説明を省くが半径をr,接線方向の速度をVとすれば
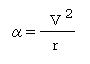
となり,円運動の向心力は
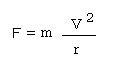
となる。物体が円運動をするためには円の中心向きに上記の力が必要である。
(2) 直線運動
ア 摩擦のない場合
① 軌道方向に力を加える。
② 力の向きに加速する → 力を加えるのをやめる → 等速直線運動
→ 移動方向と逆向きに力を加える → 速度0 → 逆向きに動くことなる。
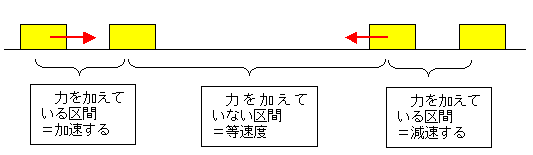
イ 摩擦がある場合
摩擦があるとき同じ運動をさせるには「まさつ中」又は「まさつ大」のボタンをクリックする。
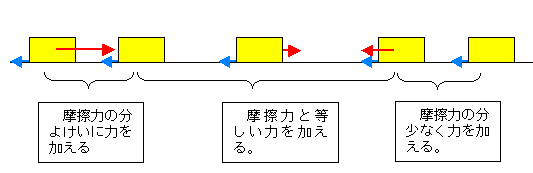
2 慣性力
(1) 円運動している乗り物の中では「遠心力」が働くのを体感することがよくある。これは加速度運動している座標系では加速度と逆向きに慣性力が働くからである。
たとえば,止まっているバスが発車するときは加速度が前向きなので,中に乗っている人には後向きに慣性力が働く。
また,ブレーキをかけたとき,加速度は後ろ向きなので,中に乗っている人には前向きに慣性力が働く。
円運動の加速度は円の中心を向いているので(力が中心向きなので)円の外向きに慣性力が働く。
円運動の場合,慣性力を遠心力と言う。また,物体に働く中心向きの力を中心力という。
(2) 慣性座標系と非慣性座標系
静止している座標系(観測者)や等速度運動している座標系では運動の法則はそのまま成り立つ。
このような座標系を慣性座標系という。そもそも静止と等速度運動は区別することはできない。
ところが,加速度運動している座標系では不思議なことが起こる。
エレベータの中や加速や減速中の列車の中,カーブを曲がりつつある車の中などでは加速度と逆向きに力が働くように感じる。
この力を慣性力といい,このような座標系を非慣性座標系という。
等速円運動は,速さは変わらないが,向きが変わるので加速度運動である。
加速度の向きは円の中心を向いており,したがって,中に乗っている人にはカーブの外向きに慣性力(遠心力)が働くことになる。