育てたい資質や能力
1 高いところにある物体は位置エネルギーをもつという見方や考え方を育てる。
2 位置エネルギーは高さと質量の積に比例するという見方や考え方を育てる。
学習のポイントと配慮事項
1 斜面においては摩擦により位置エネルギーが失われる点に配慮する。
2 厳密には重力のした仕事は注射器の縮んだ距離も加える必要がある。
3 記録タイマーのテープとしてビデオテープを使用したが,すべりがよく巻き癖がついていないなどの利点がある。
放電式記録タイマーなど正確なものがあればそれでもよいが,構造が簡単で仕組みの分かりやすい方が望ましい。
パソコンとセンサーの組合せも考えられるが,ブラックボックスでない記録タイマーのほうが望ましい。
理論的な背景
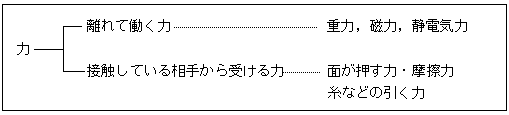
1 力の分類
自然界には次の四つの,力の相互作用がある。
① 万有引力
質量をもつ物体間に働く。地球の近くでは重力といい,地表付近では同じ質量の物体には一定の力となる。
② 電磁力
電荷どうしの間には力が働く。動く電荷は磁界をつくる。動く電荷は磁界から力を受ける。
③ 強い力
原子核を作っている力。陽子や中性子をつないでいる力。クオーク間に働く力。
原子の集まりであるいろいろな物体が壊れないおおもとの原因はこの強い力による。
④ 弱い力
原子核が崩壊するときに働く力。
* 中学生にとっては重力と強い力に起因する接触している物体間に働く力を考えればよい。
したがって,次のように分類できる。
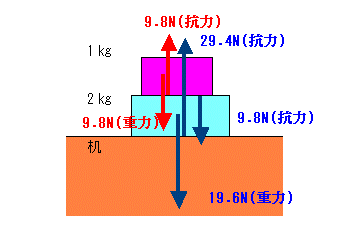
2 力のつり合い
地球上の物体には必ず重力が働く。したがって力のつり合いを考えるときには,まず重力を考え,次に何と接触しているかを考えればよいことになる。
つり合っていれば必ず力のベクトル和が0となる。
また,重力は物体の質量によって決まるので,上に他の物体が乗っていようがいまいが関係ない。
下図で赤の矢印は上の物体に働く力,青の矢印は下の物体に働く力。
3 力がつり合っていないとき
力がつり合っていないと物体には速度の変化すなわち加速度が生じる。
静止している物体は動き始める。等速度運動をしていた物体はがさらに速くなる。
等速度運動をしていた物体はとまる。等速度運動していた物体の向きが変わる...などの現象が生じる。
このとき同じ力が働いても物体により,生じる加速度は様々である。
このとき加速のさせにくさを表す量が質量である。
すなわち質量は,その物体に働く合力と生じた加速度を基に
質量=合力÷加速度
となる。合力が同じとき,生じる加速度が大きいほど質量は小さいことになる。これを慣性質量という。
質量m(㎏),加速度α(m/s2),力F(N)とすれば,
F=mα ①
と書ける。(ニュートンの運動の第二法則)
また,質量は地球上の物体に働く力を基に求めることができる。
地球上では重力だけが働く場合,物体にはおよそ10 m/s2の加速度が生じる。
したがって,物体に働く重力(N単位)を9.8で割れば質量が求められる。(力の単位が㎏重ならば,数値はそのままで単位を㎏に変えるだけ。)
こうやって求めた質量を重力質量という。もちろん慣性質量と一致する。
4 エネルギーの原理
加速度αと速度V,初速度v,変位Sの間には次の関係がある。
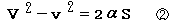
①②よりαを消去すると
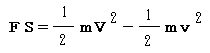
となる。
左辺の「力」×「距離」を仕事,右辺の「質量」×「速度の二乗」÷2を運動エネルギーと言う。
つまり,物体になされる仕事の分だけ物体の運動エネルギーは増加することになる。
5 重力のする仕事は物体の移動経路によらず高さの差による。
仕事Wは一般に,物体に働く力Fと物体の移動距離Sと,FとSのなす角θを用いて
W=FScosθ
で表される。
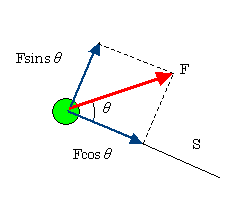
移動方向の力の成分FScosθが仕事をし,移動方向に垂直な成分FSsinθは仕事をしない。
また,θが90°を超えると仕事は負になる。摩擦力のする仕事などかこれに相当する。したがって
「仕事」=「力の移動方向への成分」×「移動距離」
となる。
また,FScosθを下図のように解釈すれば
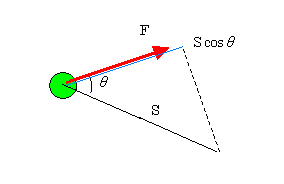
「仕事」=「力」×「力の向きへの移動距離」
となる。
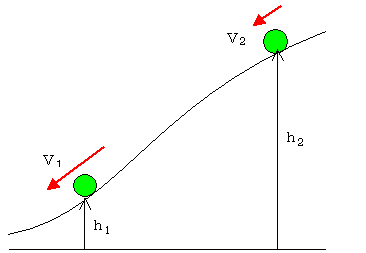
したがって上図において重力が物体にする仕事は,重力加速度をgとして
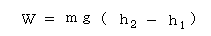
となる。
エネルギーの原理より運動エネルギーの変化は物体になされた仕事の総和に等しく,面の垂直抗力は移動方向に直角なので
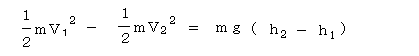
となる。さらに初速が0ならば
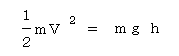
となる。
6 運動量と力積
加速度は単位時間における速度の変化と定義される。
初速度をv,加速度をαとすれば,時間をtにおける速度は
V=v+αt ④
となる。①②よりαを消去すれば
Ft=mV-mv
となる。
「力」×「時間」を「力積」,「質量」×「速度」を「運動量」と言う。
このことから物体の速度を同じだけ変えるには「力」×「時間」の積が等しいことが分かる。
つまり大きな力と短い時間,小さな力と長い時間のどちらでもその積が等しければ速度の変化は等しくなる。