1 金星の形と大きさはどのような関係があるだろうか?

◎ 金星モデルの画面上の大きさと距離の関係を調べる。
(1) 金星モデルを軌道上のいろいろな位置に置いて,カメラのズームを使わないで撮影する。
(2) 写真(画像)を同じ大きさでプリントアウトして,撮影時の金星モデルの位置にはる。
(いろいろな大きさの金星モデルの写真ができる)
(3) カメラから金星モデルまでの位置と,金星モデルの見かけの直径を定規ではかる。
(4) 距離を横軸に,見かけの直径を縦軸にしてグラフをかく。
(半比例のグラフができる。)
(5) 写真に方眼トレーシングペーパーをあてて金星モデルの昼の部分(夜の部分)の見かけの面積がどのように変化するか調べる。
(三日月状の時が最も面積が大きい・・・このときもっとも明るくみえる。)
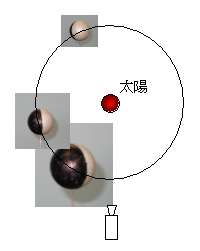
金星までの距離は内合(0.3天文単位)から外合(1.7天文単位)まで5倍以上変化するため,大きさも劇的に変化する。
2 本当に金星は満ち欠けをしているのだろうか?

◎ 金星を実際に観察する。
(1) 天文暦(理科年表・天文年鑑)などで,金星がいつどこに見られるかを調べる。
東方最大離角のときは夕方の西の空で輝く(よいの明星)。
西方最大離角のときは明け方の東の空に見える(明けの明星)。
※2003年は5月まで「明けの明星」として見えている。
「よいの明星」として夕方の空に見られるのは2003年10月以降である。
(2) 空に金星を見付けたら,低倍率(20倍程度)の天体望遠鏡で観察する。
低倍率では金星の形まではわからない。
(3) 倍率を50倍以上に上げて観察する。
金星の形を確認してスケッチする。
※ 金星はとても小さいので,形を観察するには天体望遠鏡が必需である。
3 金星までの距離を求めることはできないだろうか?

◎ 最大離角の時の角度から,金星までの距離を推定する。
関数電卓があれば,EV=SE×sin(∠SEV)で求めることができる。